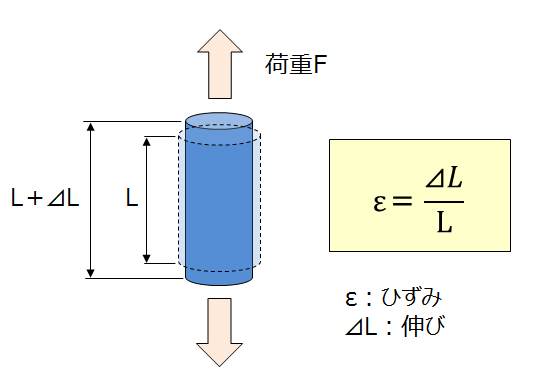
荷重が作用すると物体は変形します。変形前の長さに対するその時の変形量の割合がひずみ(歪/strain)です。引張荷重により元の長さLの物体が、⊿Lだけ伸びた時のひずみはε=⊿L÷Lで計算することができます。単位はつけないか、100倍して%で表します。
荷重が加わった時にどのように変形するかは、材料によって大きな違いがあります。強度設計においては、その違いをよく把握した上で、材料選定することがとても大切です。荷重と変形の関係を考える際、変形量の大きさだけを見てしまうと、材料の特性を正確に把握することができません。変形量の割合であるひずみで考える必要があるのです。
以下の例で説明しましょう。
同じ直径・材料で長さが異なる丸棒に、同じ大きさの引張荷重を加えてみます。

2つの丸棒の変形に違いが生じるでしょうか?
答えは以下の表のようになります。
表.長さ違いの丸棒の伸び
| 変形量 | 応力 | ひずみ | |
| 長さ20mmの丸棒 | 0.26mm | 39.8MPa | 0.013 (1.3%) |
| 長さ10mmの丸棒 | 0.13mm | 39.8MPa | 0.013 (1.3%) |
同じ大きさの荷重でも、長い丸棒の方が大きく変形することが分かります(計算方法は下記のページを参考にしてください)。一方、変形量の割合であるひずみは同じ値になります。大きく変形した長い丸棒の方が壊れやすいかというと、そうではありません。発生している応力は同じだからです(荷重F÷断面積Aなので発生応力は長さと無関係)。
技術計算ツール 「棒材の引張/圧縮荷重による応力、ひずみ、変形量の計算」
したがって、荷重により物体が変形した時、それがどのような意味を持つかは、変形量の大きさではなく変形量の割合であるひずみを見る必要があるのです。実際、強度設計の実務においても、応力とひずみの関係を表した応力-ひずみ曲線(S-S曲線)や、プラスチック材料のソルベントクラックに対する耐性を表す臨界ひずみなど、様々な場面で使われている考え方です。
スポンサードリンク
【参考文献】
JIS K7161-1:2014 「プラスチック−引張特性の求め方-第 1 部:通則」
<設計者のためのプラスチック製品設計>
関連記事&スポンサードリンク

