物体に荷重(外力)が作用すると、その荷重とつり合う大きさの力が物体の内部に発生します。この発生した力(内力)のことを応力(stress)といいます。
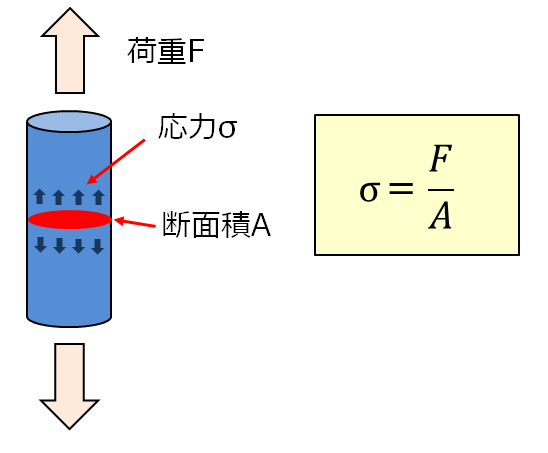
応力は単位面積当たりに作用する力を表すため、上図のような丸棒の引張荷重の場合、応力σ=荷重F÷断面積Aとなります。単位はN/mm2やMPaなどを使います。
強度設計では荷重の大きさよりも、物体に発生する応力をしっかり見ることが重要です。その理由を下記の例で考えてみましょう。
50Nの荷重が掛かっている直径4mmの丸棒と20Nの荷重が掛かっている直径2mmの丸棒があります。どちらの方がより厳しい条件でしょうか。
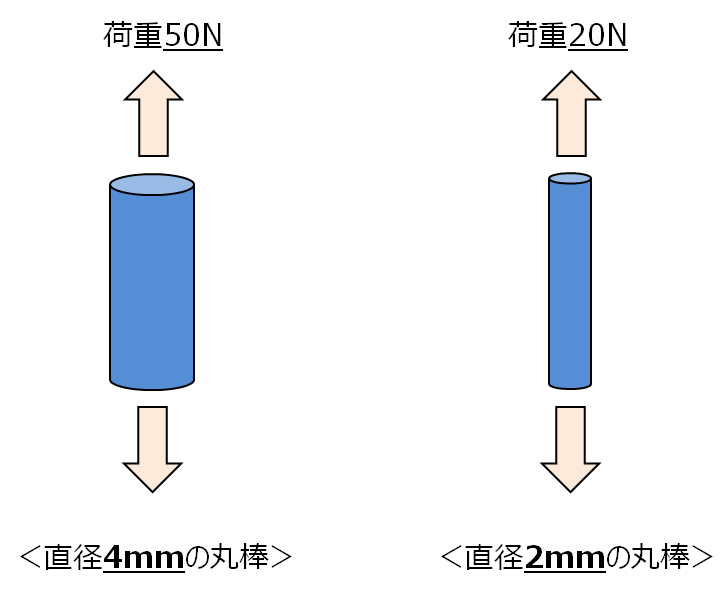
荷重の大きさだけで考えた場合、直径4mmの丸棒の方が厳しい条件のように感じられます。もちろん荷重の大きさだけで比較できないことは直感的に分かるはずです。上図の場合、丸棒内部に発生している応力は以下のようになります。
表.丸棒に発生する応力
| 断面積 | 応力 | |
| 直径4mmの丸棒 | 12.57mm2 | 3.98N/mm2(またはMPa) |
| 直径2mmの丸棒 | 3.14mm2 | 6.37N/mm2(またはMPa) |
直径2mmの丸棒に発生する応力の方が、直径4mmの丸棒に発生する応力より約1.6倍大きいことが分かります。荷重が小さい直径2mmの丸棒の方が厳しい条件なのです。このことから、強度設計を行う場合、荷重の大きさよりも物体に発生する応力の方が重要なことが理解できると思います。
材料の強度は応力で表されます。ABSの物性表を見てみましょう。
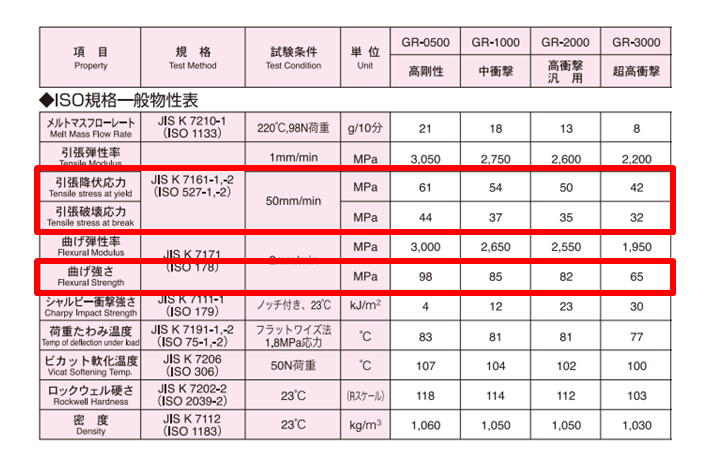
デンカ株式会社 「デンカABS 一般物性表」を改変
(出所:デンカ株式会社HP)
http://www.denka.co.jp/resin/product/pdf/abs.pdf 2017年3月16日
赤枠で囲った部分の数値以上の応力が材料に発生した時、壊れるということを意味しています。MPa=N/mm2ですので、例えば「GR-0500」というグレードのABSは、44N/mm2、すなわち1mm2当たり44Nの引張荷重が加わると壊れるということを示しています。
※「壊れる」ことをどう定義するかによってこれらの数値は異なります。この物性表では引張強度を「引張降伏応力」と「引張破壊応力」の2つで表しています。
スポンサードリンク
以下で丸棒と角棒の引張、圧縮応力を計算できますので、チェックしてみてください。
【丸棒の引張/圧縮応力計算】

| 荷重 F(N) | 50 | 半角数字を入力してください(F>0) |
| 直径 d(mm) | 5 | 半角数字を入力してください(d>0) |
| 応力 σ(MPa or N/mm2) | 2.546 | 計算結果 |
【角棒の引張/圧縮応力計算】

| 荷重 F(N) | 50 | 半角数字を入力してください(F>0) |
| 長さ a(mm) | 5 | 半角数字を入力してください(a>0) |
| 長さ b(mm) | 5 | 半角数字を入力してください(b>0) |
| 応力 σ(MPa or N/mm2) | 2 | 計算結果 |
スポンサードリンク
<設計者のためのプラスチック製品設計>
関連記事&スポンサードリンク

