荷重を掛けると変形し、荷重を取り除くと元に戻るような物質を弾性体、そのような変形を弾性変形といいます。弾性体に荷重を加えると、発生する応力σとひずみεは比例の関係になります。引張荷重を掛けた時を例に見てみましょう。
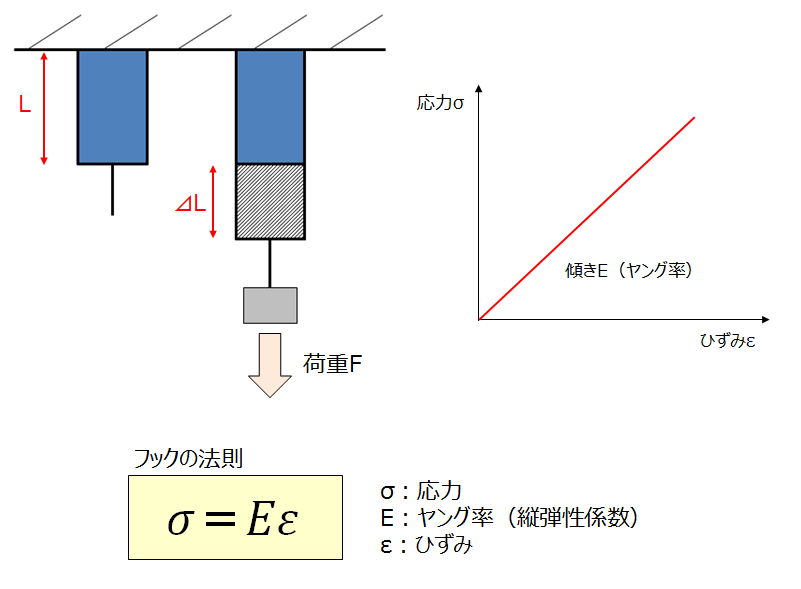
このような関係が成り立つことをフックの法則といいます。垂直荷重(引張または圧縮荷重)を掛けた時、この直線の傾きはヤング率または縦弾性係数と呼ばれ、物体を変形させるのに必要な力の大きさを示す指標となります。単位はMPa(またはGPa)が使われます。
少し分かりにくいと感じる方は、中学校や高校で勉強したばねを思い出してください。考え方は全く同じです。

ばねに荷重Fを掛けた時、元の長さからxだけ伸びたとすると、F=kxという式で表すことができました。これもフックの法則です。荷重Fが応力σ、ばね定数kがヤング率E、ばねの伸びxがひずみεに相当します。
上記では引張荷重を例に説明しましたが、弾性体ではせん断荷重でも同様にフックの法則が成り立ちます。せん断荷重ではせん断応力τ(タウ)、せん断ひずみγ(ガンマ)が比例関係になります。

Gは横弾性係数またはせん断弾性係数と呼ばれます。単位はヤング率と同じMPa(またはGPa)です。横弾性係数は強度設計の実務ではあまり使いません。等方性材料ではヤング率(縦弾性係数)とポアソン比が分かれば、横弾性係数を導くことができるからです。以下の記事で計算ツールを作っていますので、使ってみてください。
<参考記事>
技術計算ツール 「横弾性係数換算式」
スポンサードリンク
プラスチックのヤング率
プラスチックのヤング率はどの程度でしょうか。普段の生活でも分かるように、プラスチックは金属と比べると簡単に変形します。すなわちヤング率が低いのです。以下の図でプラスチックとその他の材料のヤング率を比較しています。
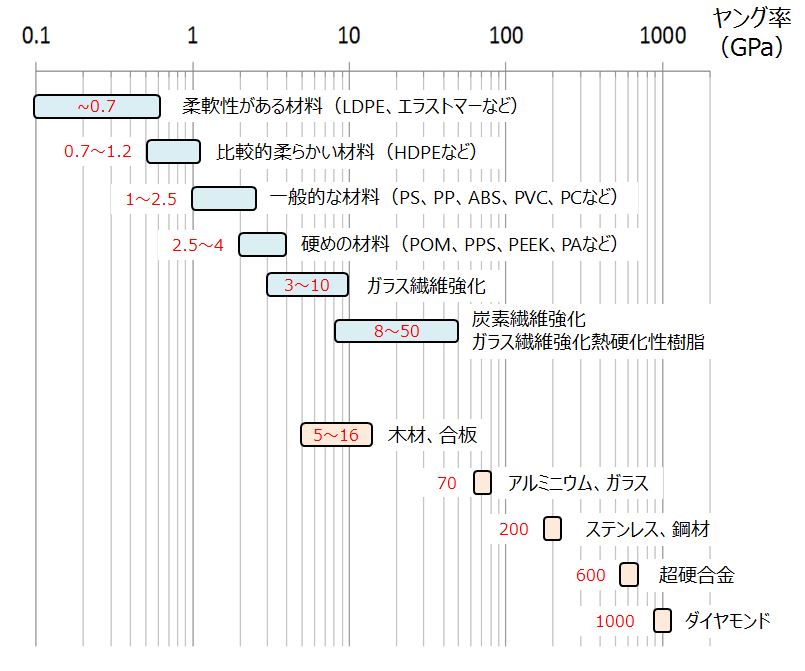
※プラスチックのヤング率はMPaで表現されることが多いですが、下記では金属との比較のために、GPaに統一しています。
※「ヤング率比較」作成にあたって参考にした企業・団体のwebサイトおよび参考資料
日本ポリエチレン株式会社/株式会社プライムポリマー/旭化成株式会社/日本ポリエチレン株式会社/住友化学株式会社/PSジャパン株式会社/東レプラスチック精工株式会社/デンカ株式会社/UMGABS株式会社/テクノポリマー株式会社/帝人株式会社/東洋紡株式会社/DIC化工株式会社/国立研究開発法人物質・材料研究機構/日本板硝子株式会社/日本合板工業組合連合会/日本タングステン株式会社/オグラ宝石精機工業株式会社/理科年表2016
金属と比較すると、通常のプラスチックで2桁、強化プラスチックで1桁、ヤング率が低いことが分かります。このことは、同じ形状のものであれば、同じ長さだけ変形をさせるのに、プラスチックは金属の1/10~1/100の力で変形させることができるということです。変形しやすいことにはメリットもデメリットもありますので、プラスチックの特性をよく理解して使用することが大切です。
スポンサードリンク
プラスチックのヤング率を考える時の注意点
①同じ原料でもグレードによりヤング率は異なる
プラスチックは同じ原料(例えばABS)でも、グレードによる違いや、配合剤、特にガラス繊維などによる強化で、ヤング率に大きな違いを生じます。以下の表はABSのグレードによるヤング率の違いです。
ABSグレード 引張弾性率(MPa) GR-2030G ガラス繊維強化(30%) 7980 GR-2020G ガラス繊維強化(20%) 5860 GR-2010G ガラス繊維強化(10%) 3920 GR-0500 高剛性 3050 GR-2000 汎用 2600 K-090 耐熱 2600 GR-3000 衝撃 2200
出所:デンカ株式会社「ABS樹脂総合カタログ」を元に作成
一般的に耐衝撃性グレードはヤング率が低下します。また、ガラス繊維や炭素繊維で強化すると、その含有量に比例してヤング率を大きくすることができます。
②温度が上がるとヤング率は大きく低下する
プラスチックのヤング率は温度上昇とともに低下していきます。物性表に記載されているヤング率は室温(23℃:JISK7161-1)で測定した値ですので、使用する環境がそれよりも高い温度の場合は、ヤング率を低めに見積もる必要があります。
③プラスチックは弾性体とみなせる範囲が狭い
弾性体とみなすことができるのは、応力やひずみが小さい場合(比例限度内)に限られます。また、応力の作用する時間が長くなると、弾性体とみなすことができなくなることもあります。プラスチックは、弾性体とみなせる範囲が非常に狭いのが特徴です。大きな変形や長期間に渡って応力が作用するような場合には、弾性体として考えると誤差が大きくなってしまうので、注意が必要です。
ひずみや変形量を計算してみよう
フックの法則を学ぶことにより、ひずみや変形量を計算することができます。以下で丸棒の計算をしてみましょう。
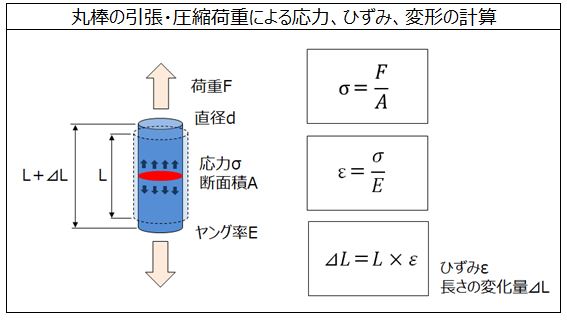
荷重 F(N) 500 半角数字を入力してください(F>0) 直径 d(mm) 4 半角数字を入力してください(d>0) ヤング率 E(MPa) 3050 半角数字を入力してください(E>0) 長さ L(mm) 20 半角数字を入力してください(L>0) 断面積 A(mm2) 12.566 計算結果 応力 σ(MPa) 39.789 計算結果 ひずみ ε 0.013 計算結果 変形量 ⊿L(mm) 0.261 計算結果(引張:伸び量、圧縮:縮み量)
スポンサードリンク
以下のサイトで角棒の計算をすることができます。
技術計算ツール 「棒材の引張/圧縮荷重による応力、ひずみ、変形量の計算」
【参考文献】
日本機械学会(編) 『機械工学便覧 基礎編 材料力学』
JIS K7161-1:2014 「プラスチック−引張特性の求め方-第 1 部:通則」
<設計者のためのプラスチック製品設計>
関連記事&スポンサードリンク

