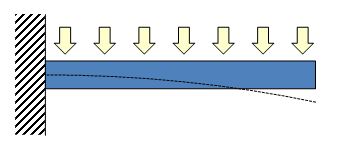
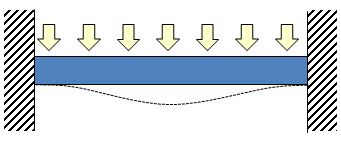
前回は、はりにどのような応力が発生しているかについて解説しました。
今回は、はりに発生している応力やたわみを実際に計算します。
はりの強度計算では様々な値を求めることができます。一般的にプラスチックの強度設計においては、以下の値を求めたいことが多いでしょう。
・最大応力(曲げ応力)
・最大ひずみ
・最大たわみ
片持ちはりを例に考えてみましょう。
片持ちはりに荷重が作用すると、以下のように応力とたわみが発生します。
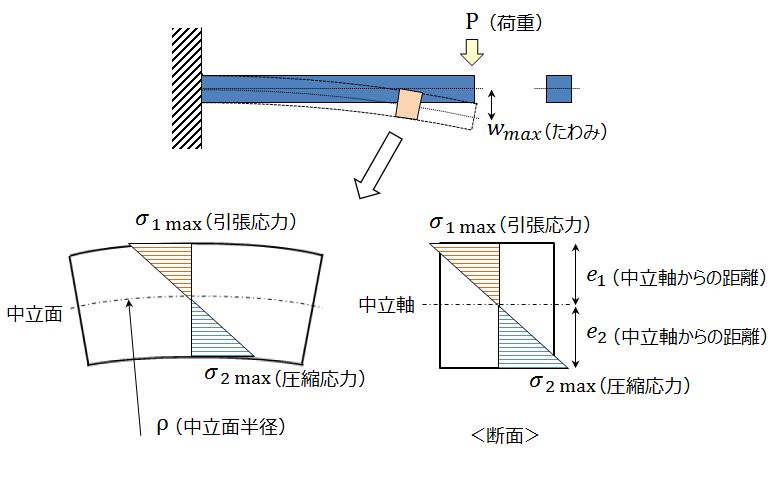
はりに荷重が作用すると中立面は円のようにたわみます。その時の中立面の半径をρ、中立軸から上下端面までの距離をそれぞれe1、e2とすると、応力σとひずみεは以下のように計算することができます。

※上記の式ははりの種類、断面形状によらず同じです。
<応力σ>
はりに作用している曲げモーメントMを、断面係数Zで割ることにより求めることができます。断面係数ははりの断面形状のみで決まります。最大応力は中立軸から最も離れた端面で発生します。はりの断面形状が中立軸に関して対称の場合、上下端面で生じる応力は同じ大きさですが(引張と圧縮で向きは反対)、非対称の場合は中立軸からの距離eが大きい方の端面で、より大きな応力が発生します。
<ひずみε>
フックの法則σ=Eεより、応力σとヤング率Eが分かれば計算することができます。最大応力が発生している部分でひずみも最大になります。はりの強度計算は弾性変形を前提にしています。プラスチックは弾性変形範囲が狭いため、ひずみの大きさを知ることは大切です。一般的にひずみの大きさが1%を超える場合、弾性変形範囲を超えていることが多いので、その時は精度の高い計算をすることができません。
また、ひずみが生じているプラスチックは、ソルベントクラックに注意する必要があります。ソルベントクラックは一定以上のひずみ(臨界ひずみ)が生じている部分に溶剤や薬品が付着することによって起こります。特にABSのような非晶性プラスチックで注意が必要な現象です。はりの強度計算でひずみを知ることができれば、ソルベントクラックの予防に役立てることができます。
<たわみ(変形量)w>
たわみは中立面半径ρを使って計算することにより求められます。はりの種類毎に計算式があります。中立面半径が大きいとたわみは小さくなりますので、EIが大きいほどたわみにくいはりであることを意味します。そのためEIははりの曲げ剛性とも呼ばれます。
スポンサードリンク
断面二次モーメントと断面係数
断面二次モーメントIと断面係数Zは、いずれもはりの断面形状によって決まる係数です。
長方形断面の断面二次モーメントと断面係数を見てみましょう。
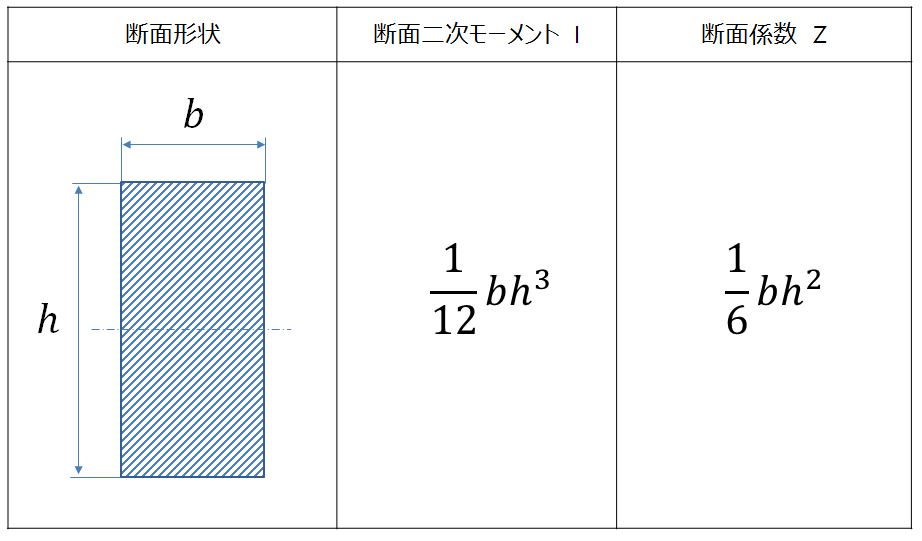
長方形断面は中立軸に関して対称ですので、端面までの距離は上下どちらも同じです。したがって、断面係数の値は一つしかありません。EIが曲げ剛性を表しますので、断面二次モーメントが大きいほど、変形しにくくなります。計算式を見ると、断面二次モーメントは幅b、高さhの3乗に、断面係数は幅b、高さhの2乗に比例することが分かります。これははりの剛性や強さを高めようと思えば、幅bを大きくするよりも、高さhを大きくした方が、圧倒的に高い効果があることを意味しています。プラスチック製の定規などで、縦方向と横方向の剛性・強さが全く違うことや、プラスチック製品がリブを多用している理由が理解できると思います。
次に三角形断面を見てみましょう。
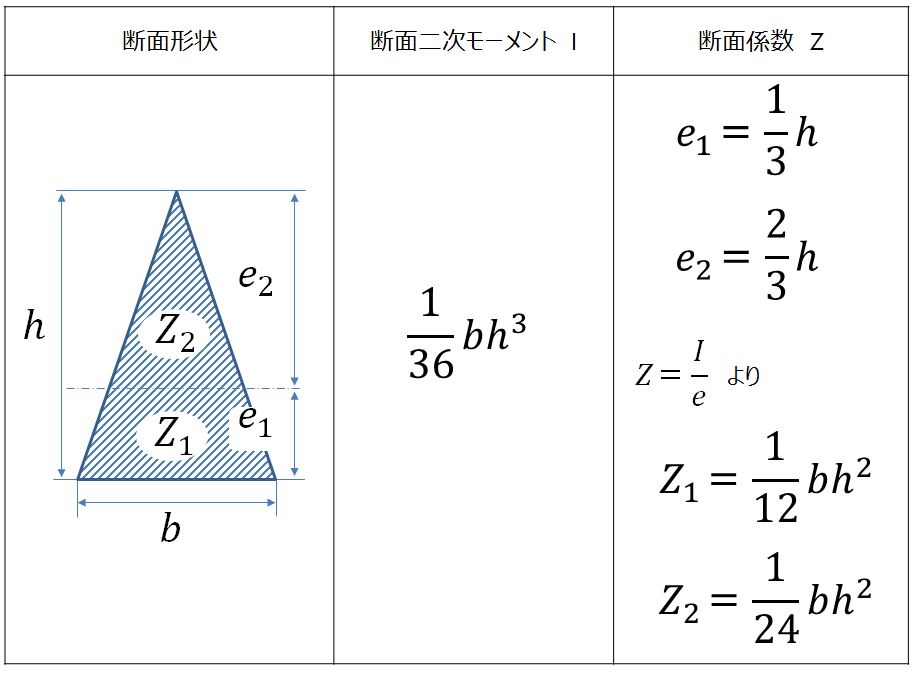
三角形断面の場合は、中立軸に関して非対称ですので、端面までの距離が上下で異なります。したがって、断面係数が2つ存在します(断面二次モーメントは1つしかありません)。発生応力はσ=M/Zですので、上下端面で発生応力が異なります。断面係数が大きいほど発生応力は小さくなるので、上記の三角形断面の場合、上側の頂点部分に最も大きな応力が発生します。
※中立軸:断面の図心(重心)を通る線
スポンサードリンク
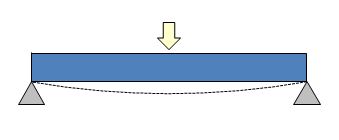
両端単純支持+集中荷重の強度計算
それでは実際にはりの強度計算をする方法を解説します。まずは両端単純支持+集中荷重の場合です。計算式は断面形状により異なりますので、今回は長方形と三角形断面の場合を説明します。
<長方形断面の場合>
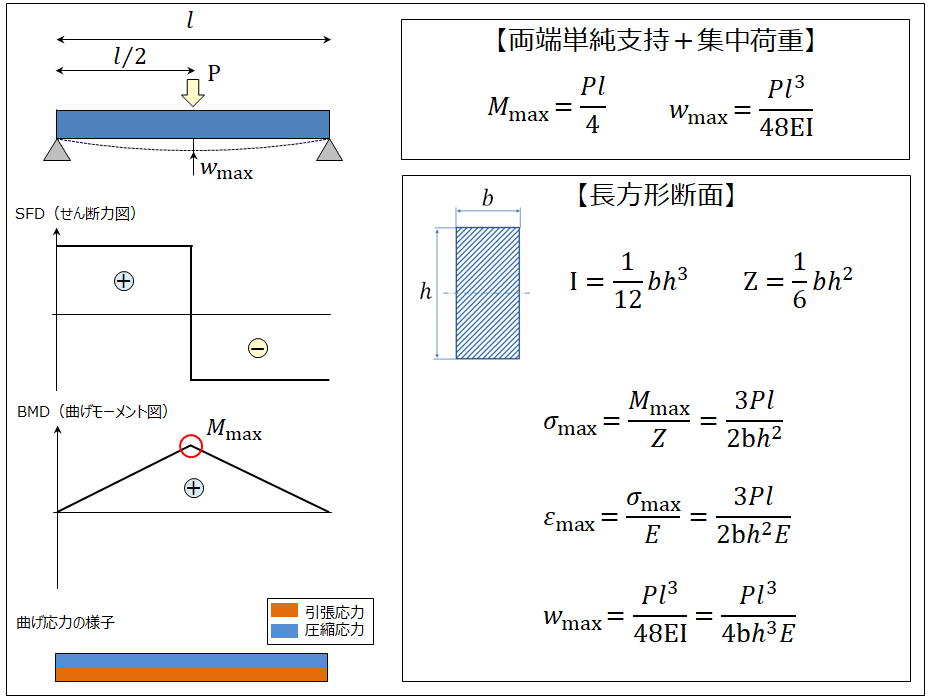
上記は両端単純支持のはりの中央部分に、集中荷重が作用したケースです。BMD(曲げモーメント図)を見ることにより、はりのどの部分に最大曲げモーメントMmaxが発生しているかを読み取ることができます。Mmaxの位置が最大応力(曲げ応力)発生位置です。はりの下面側に引張応力、上面側に圧縮応力が生じており、位置が同じであればその大きさは同じです。一般的にプラスチックは引張強度<圧縮強度ですので、はりの中央下面側が最も注意すべき部分だといえます。また、最大たわみwmaxは荷重を掛けている中央部分で生じています。
上記の計算式は「プラスチック-曲げ特性の求め方」(JIS K7171:2016)で、プラスチックの曲げ特性(曲げ強度、曲げ弾性率など)を計算する時に実際に用いられています。
サイト上で計算することができます。
はりの強度計算 【両端単純支持-集中荷重-長方形】
<三角形断面の場合>
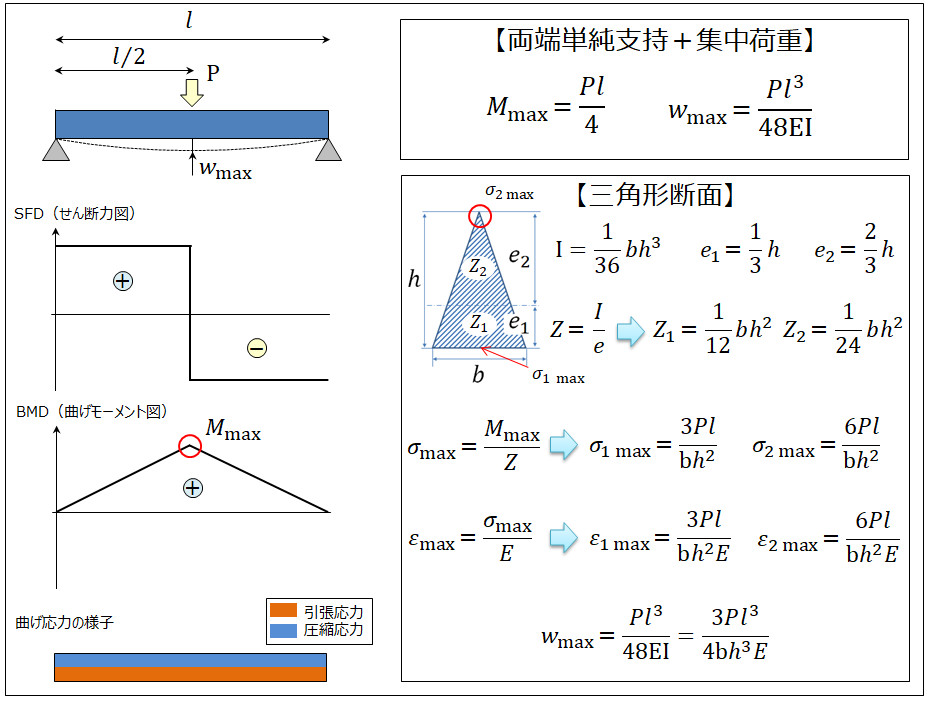
長方形断面との違いは、断面係数が2つあることです。三角形の底辺部分でσ1 max、頂点部分でσ2 maxが生じます。中立軸から端面までの距離はe2の方が大きい(断面係数はZ2の方が小さい)ので、発生応力はσ2 maxの方が大きくなります。また、σ1 maxは引張応力、σ2 maxは圧縮応力です。一般的にプラスチックは引張強度<圧縮強度ですので、上下端面のどちらがより危険であるかは、プラスチックの特性次第だといえます。
サイト上で計算することができます。
はりの強度計算 【両端単純支持-集中荷重-三角形】
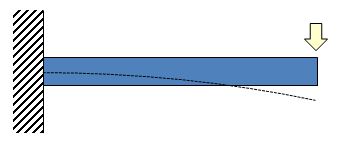
片持ちはり+集中荷重の強度計算
同様に片持ちはり+集中荷重の例を見てみましょう。
<長方形断面の場合>
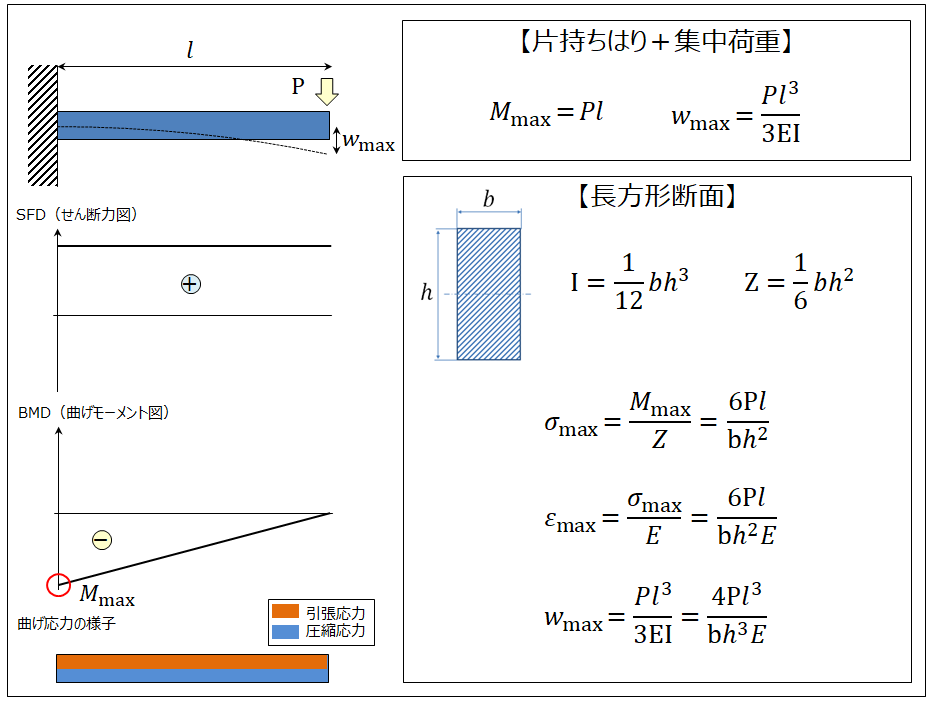
上記は片持ちはりの先端部分に、集中荷重が作用したケースです。BMD(曲げモーメント図)を見ることにより、はりの固定部根本部分に最大曲げモーメントMmax(および最大応力σmax)が生じているのが分かります。はりの下面側に圧縮応力、上面側に引張応力が生じており、位置が同じであれば同じ大きさです。一般的にプラスチックは引張強度<圧縮強度ですので、はりの固定部根本の上面側が最も注意すべき部分だといえます。また、最大たわみwmaxは荷重を掛けている先端部分で生じます。
サイト上で計算することができます。
はりの強度計算 【片持ちはり-集中荷重-長方形】
スポンサードリンク
荷重/断面形状/はりの長さが同じでも、両端単純支持よりも片持ちはりの方が発生応力もたわみも大きいことが分かります。
<三角形断面の場合>
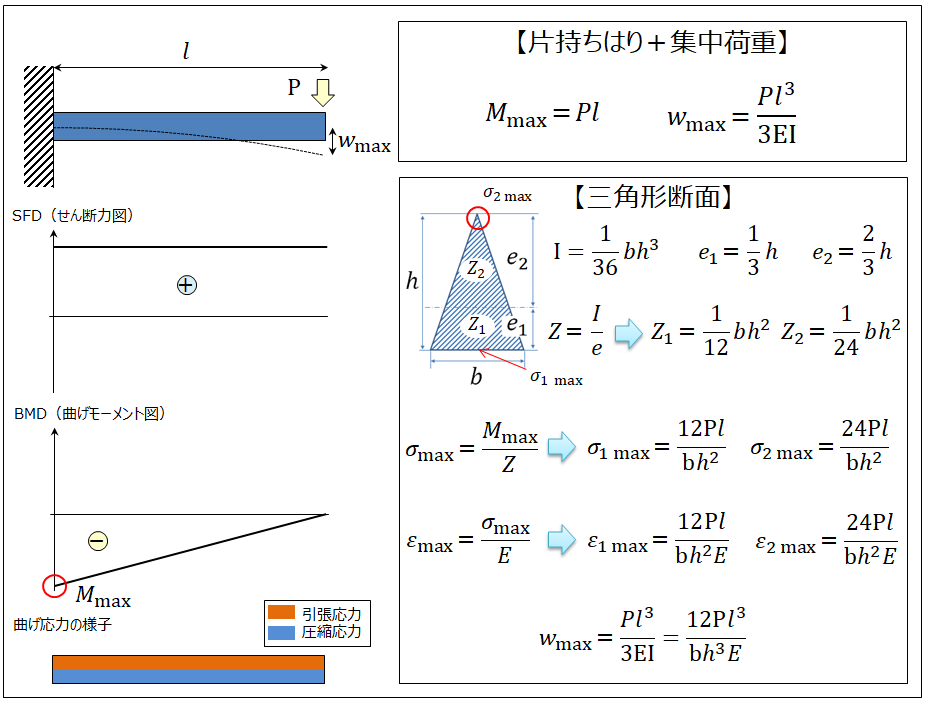
両端単純支持の場合と同様に、断面係数が二つあることに注意が必要です。
サイト上で計算することができます。
はりの強度計算 【片持ちはり-集中荷重-三角形】
スポンサードリンク
【参考文献】
日本機械学会(編) 『機械工学便覧 基礎編 材料力学』
JIS K7171-1:2016 「プラスチック−曲げ特性の求め方」
<設計者のためのプラスチック製品設計>
関連記事&スポンサードリンク