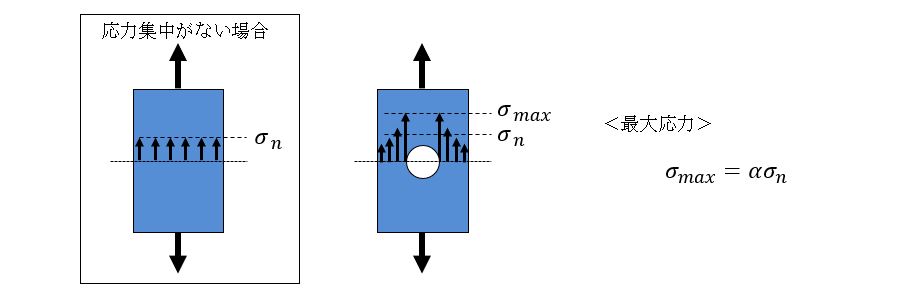
https://youtu.be/Ng8kRvNpE_U 孔や切欠、R部などの近傍で急激に応力が大きくなる現象。最大応力σmaxは公称応力σnに対する倍率である応力集中係数αで表される。公称応力とは応力集中がない場合に計算される応力のこと。
応力集中係数は条件に応じて様々な曲線を持つグラフによって示され、そこから読み取って計算する。下図は孔のある板材に引張荷重が作用している場合の応力集中の計算式とグラフである。公称応力は荷重を孔部分を除いた断面積で割って計算している。グラフは参考文献を元に作成した。
下記は孔のある板材に引張荷重を加えたときの応力集中の様子。Fusion360でシミュレーションを行った。応力集中係数はほぼグラフの値と一致する。
<孔あり板材+引張荷重>
応力集中は孔だけではなく、以下のような様々なケースがある。
<スナップフィット>
<段付き板材+引張荷重>
<段付き板材+モーメント荷重>
<段付き丸棒+引張荷重>
<段付き丸棒+モーメント荷重>
<U字切欠付板材+引張荷重>
最終更新 2020年6月11日
【参考文献】
西田正孝「応力集中(増補版)」(森北出版)
スポンサードリンク
| > 偶力 |
| > ***** |
| > 断面係数 |
| > 断面二次モーメント |
| > 中立面 |
| > トラス |
| > ***** |
| > ***** |
| > ***** |
| >> 平等強さのはり |
| > ***** |
| > 曲げモーメント |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| > ***** |
| >> SI基本単位 |
| > ***** |
| > ***** |
| > ***** |