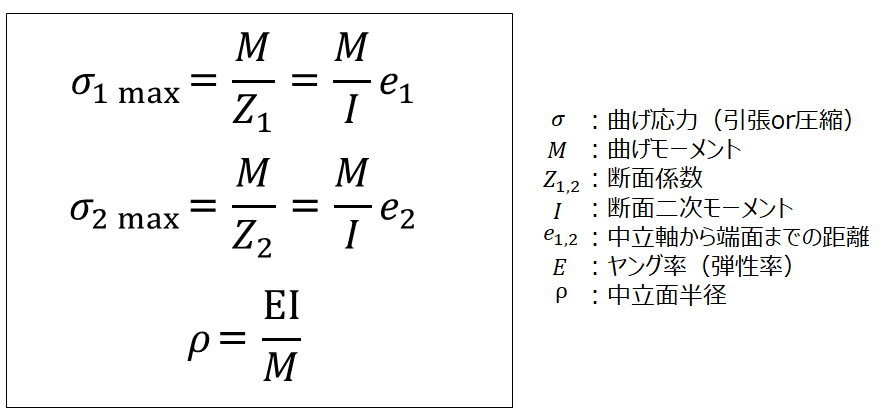2017年12月にプラスチックス・ジャパン.comに寄稿した記事を掲載します。
1. はじめに
構造解析ソフトを使った強度解析は、設計者でも容易に実施できるようになって久しい。しかし、3Dモデルの作成や境界条件の設定などに時間がかかるため、まだ電卓並みというわけにはいかない。強度解析を効率よく実施するためには、ある程度の当たり付けをした後に構造解析ソフトを使うことが望ましい。当たり付けの有力な手段がはりの強度計算である。今回ははりの強度計算について概要を解説する。
2. はりについて
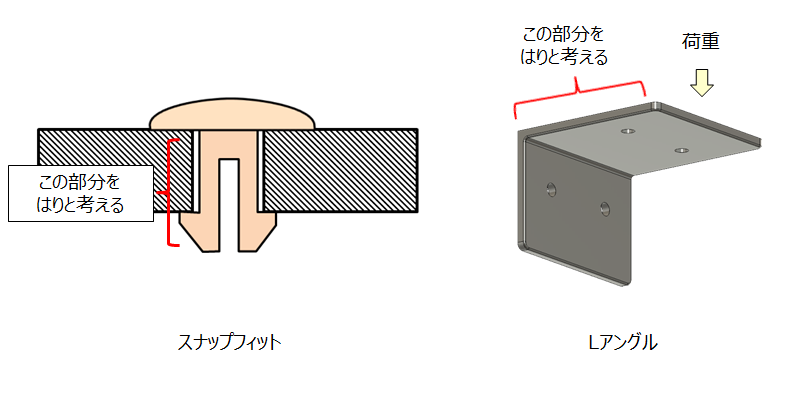
曲げ荷重を受ける細長い部材をはり(beam)という。垂直方向の圧縮荷重を受ける柱(column)と組み合わせることにより、建築や機械など様々な構造物で利用されている。プラスチック製品は一体成形されることが多いため、はりは使われていないと思うかもしれない。しかし、図1のように構造の一部をはりと考えることによって、はりの計算式を使った強度解析を行うことができる。
図1 プラスチック製品の例
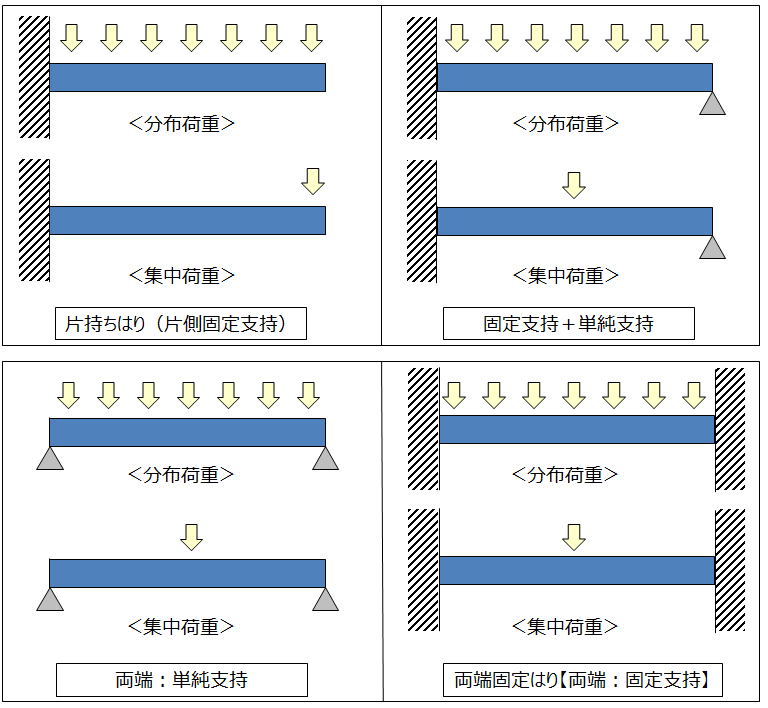
はりは荷重の種類と支持方法の組み合わせによって多くの種類が存在する(図2、図3)。
図2 荷重と支持方法の種類
図3 はりの種類
それぞれのはりごとに計算式が準備されており、断面特性、長さ、ヤング率(弾性率)を入力することにより、応力やたわみを求めることができる。
3. はりに発生する応力とたわみ
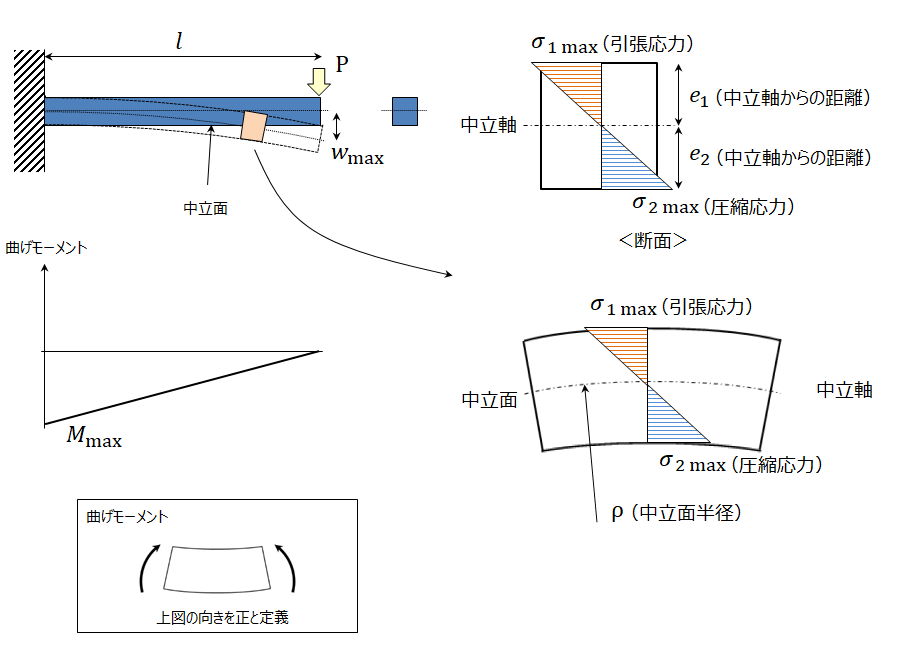
はりに発生する応力とたわみを片持ちはりを例に説明しよう。片持ちはりの先端に荷重(集中荷重)をかけると、応力σとたわみwが発生する。
図4 片持ちはりに発生する応力
はりには曲げモーメントが作用し、はりの上側に引張応力(σ1)、下側に圧縮応力(σ2)が発生する。応力は中立軸からの距離に比例して大きくなるため、はりの上下端で最大となる。
曲げモーメントははりの長さ方向でグラフのように変化する。応力は曲げモーメントの大きさに比例するため、曲げモーメントの絶対値が最大となる根本部分で最も大きな応力が発生する(※1、※2)。根本部分の上端には引張応力の最大値、下端には圧縮応力の最大値が発生するが、一般的にプラスチックは引張強度<圧縮強度であるため、上端が最も危険性の高い箇所であるといえる。また、最も大きなたわみが発生するのははりの先端部分となる(※2)。
※1 曲げモーメントは図4の向きを正と定義。反対向きに定義した場合は、根本部分の曲げモーメントは正となる。
※2 最大応力および最大たわみが発生する位置ははりの種類により異なる。
はりに発生する応力は図5の計算式で求めることができる。
図5 はりに発生する応力と中立面半径
図5の計算式ははりの種類によらず同じである。曲げモーメントが同じであれば、断面係数が大きいほど発生応力は小さくなる。断面係数ははりの形状によって決まる係数である。
たわみは中立面半径の大きさから計算される。曲げモーメントが同じであれば、ヤング率と断面二次モーメントの積EI(はりの曲げ剛性)が大きいほどたわみにくいことを表している。断面二次モーメントは断面係数と同じく、はりの断面形状で決まる係数である。
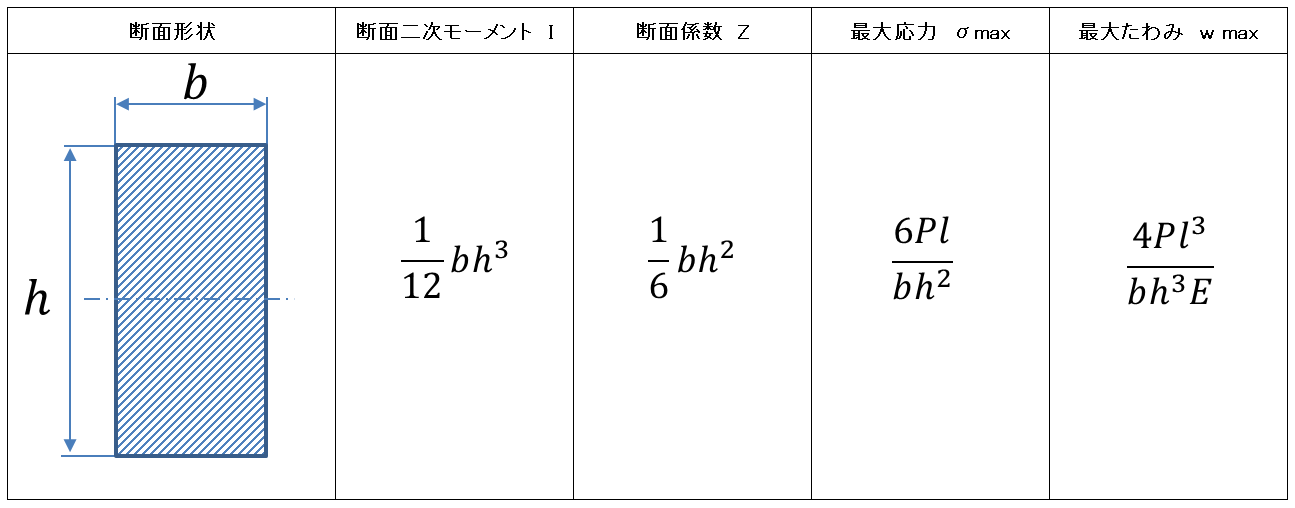
図5から導かれる長方形断面、三角形断面の計算式を表1、2に示す。
表1 長方形断面の計算式
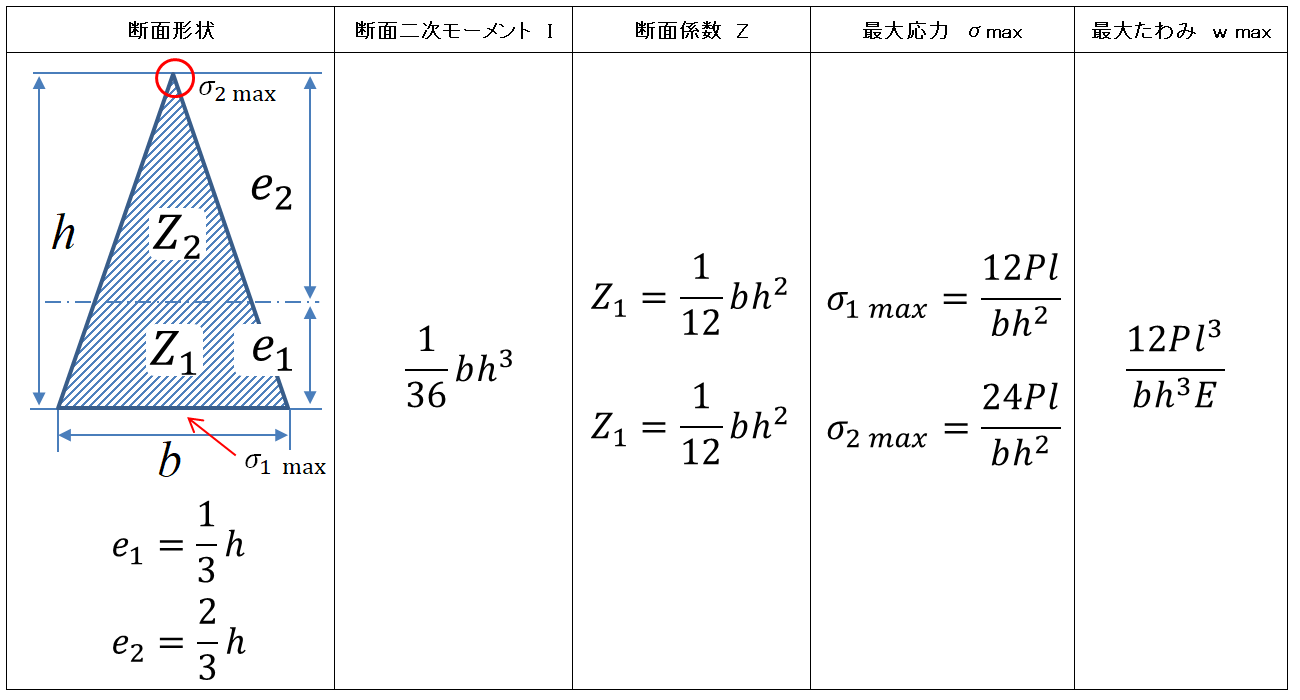
表2 三角形断面の計算式
これらの計算式ははりの種類、断面形状によってそれぞれ異なった式となる(断面二次モーメントと断面係数ははりの種類とは無関係)。
注意する必要があるのは、断面形状が中立軸に対して非対称の場合である。断面形状が長方形や円などの場合は、e1=e2であるため、σ1とσ2は同じ大きさとなる。三角形や台形など中立軸に対して非対称な形状の場合は、e1≠e2であるため、σ1とσ2も違う値となる。表2から分かるように、三角形の場合は底辺部分よりも頂点部分の方が、応力が2倍大きくなっている。
ちなみに、ヤング率と発生応力が分かれば、フックの法則σ=Eεからひずみを簡単に計算することができる。ひずみはソルベントクラックの防止や、変形が弾性変形(応力と変形が比例関係にある)の範囲に入っているかどうかの確認などに活用することができる(※3)。
※3 一般にプラスチックが弾性変形の範囲に入ると考えてよいのは、ひずみが1%程度までといわれている。はりの強度計算は材料が弾性変形することを前提にしているため、1%を大きく超えた場合は精度が低くなる。
4. 実際の活用事例
スナップフィットを例に考えてみよう。スナップフィットはプラスチック部品同士の締結用に様々な製品で使われている(図6)。
図6 スナップフィット
スナップフィットをよく見ると、片持ちはりに見えてこないだろうか。図6のスナップフィットを図7のような片持ちはりだと考えてみよう。
図7 スナップフィットと仮定
図7のスナップフィットは、先端の段差部分(1.25mm)を変形させることによって、相手側にはめ込まれる。したがって、1.25mm変形させた時に不具合が起きないように設計する必要がある。
1.25mm変形させたときに発生する応力は、表1のはりの計算式から簡単に導くことができる。ひずみはフックの法則から計算した。
表3 スナップフィットに発生する応力
すなわち、1.41Nの荷重を与えれば、スナップフィットの先端部分が1.25mm変形することが分かる。この時に発生する応力やひずみを確認し、問題が発生しないかどうかを検討すればよい。
※4実際にはR部分に応力集中が生じるため、Rの大きさよっては計算式よりもかなり大きな応力が発生する。( )内は応力集中係数を1.35(理論値よりも1.35倍大きくなる)として計算した値。
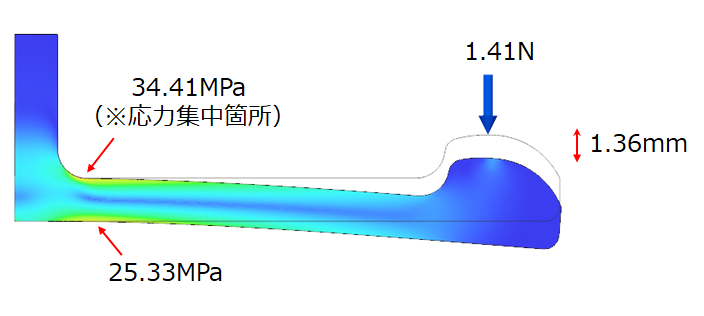
構造解析ソフトでシミュレーションすると図8のようになる。
図8 スナップフィットの強度解析
1.41Nを加えると、1.36mm変形し、上側は応力集中が起きるので34.41MPa、下側は25.33MPaが発生している。多少の誤差はあるものの、当たり付けとしては十分使えるレベルだろう。
5. おわりに
はりの強度計算について概要を解説した。スナップフィット以外にも、リブの形状の検討や筐体の厚みの比較など、様々な場面で活用することができる。プラスチック製品の強度設計のスピードアップと品質向上にぜひ役立ててほしい。
【参考文献】
日本機械学会(編) 『機械工学便覧 基礎編 材料力学』
村上敬宜 『材料力学』 森北出版
西田正孝(著) 森北出版 『応力集中 増補版』