スポンサードリンク
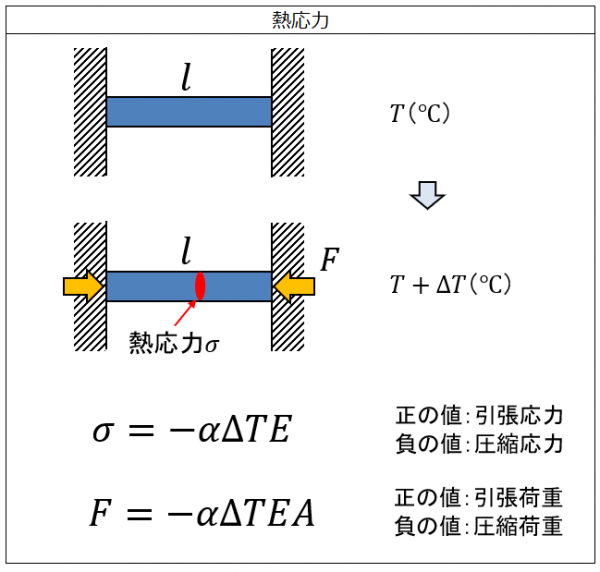
熱応力σは両端に壁がなければ生じる寸法変化Δlを、力Fを加えて元の長さまで戻すことによって生じると考えます。
フックの法則、力と応力の関係より、
\(σ= εE\)・・・①
\(F= σA\)・・・②
ですので、物体に生じているひずみεが分かれば、熱応力と生じる力を導くことができます。
温度変化により物体の長さはl⇒l+Δlになったので、
\(ε=-\frac{Δl}{l+Δl}\)・・・③
となります(圧縮方向なので符号はマイナス)。
Δlは線膨張係数αを使って以下のように表すことができます。
\(Δl= αΔTl\)・・・④
④を③に代入すると、
\(ε=-\frac{αΔTl}{l+αΔTl}\)・・・⑤
分母分子をlで割ると、
\(ε=-\frac{αΔT}{1+αΔT}\)・・・⑥
αは非常に小さな値(αT≪1)ですので、1+αΔT≒1と近似することができます。
\(ε=-αΔTl\)・・・⑦
①、②、⑦より
\(σ=-αΔTE\)・・・⑧
\(F=-αΔTEA\)・・・⑨
少し不思議な感じもしますが、熱応力と生じる力は、物体の長さに無関係であることが分かります。
スポンサードリンク
<参考文献>
日本機械学会(編) 『機械工学便覧 基礎編 材料力学』
最終更新 2019年6月28日