| 『図解! わかりやすーい 強度設計実務入門 基礎から学べる機械設計の材料強度と強度計算』(日刊工業新聞社) 田口宏之(著)※本サイト運営者 |
| 強度設計をしっかり行うには広範囲の知識が必要です。本書は、多忙な若手設計者でも強度設計の全体像を効率的に理解できることを目的に執筆しました。理論や数式の導出は最低限にとどめ、たくさんの図を使って解説しています。 |
スポンサードリンク
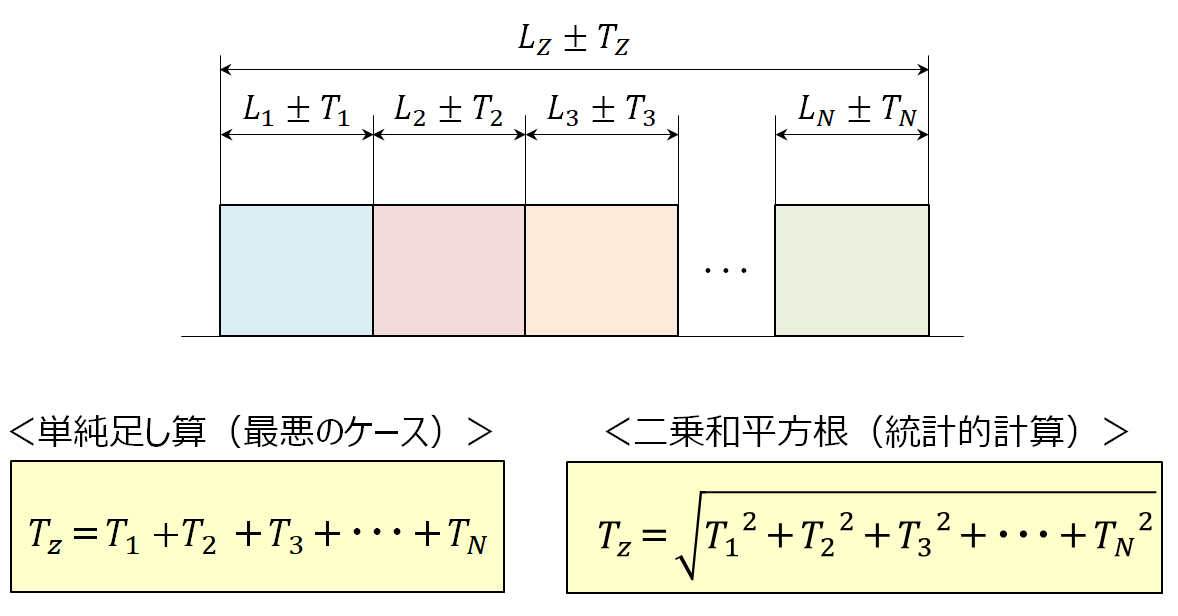
累積公差を検討する場合、公差を単純に足し合わせた最悪のケースを考えておけば、問題が発生することはほとんどない。しかし、組み合わせる部品の個数が増えてくると、無駄な製造コストがかかってしまう。そのため累積公差を統計的に計算する方法を採用することが多い。
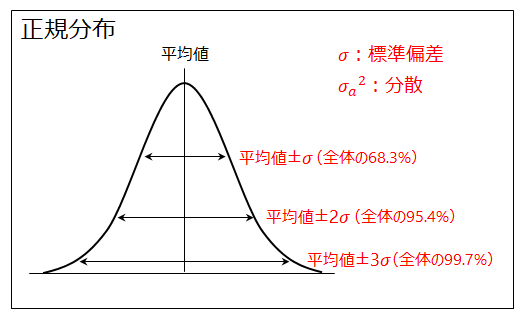
各部品の寸法は十分に管理され、その分布が平均値を中心とした正規分布となっていると仮定する。この時のバラツキの程度を示すのが標準偏差σ、標準偏差の2乗が分散である。平均値±σの範囲内に全体の68.3%、平均値±2σの範囲内に全体の95.4%、平均値±3σの範囲内に全体の99.7%が入る。一般的に寸法は±3σの中に入るように管理されていることが多く、その場合の不良率は0.3%となる。
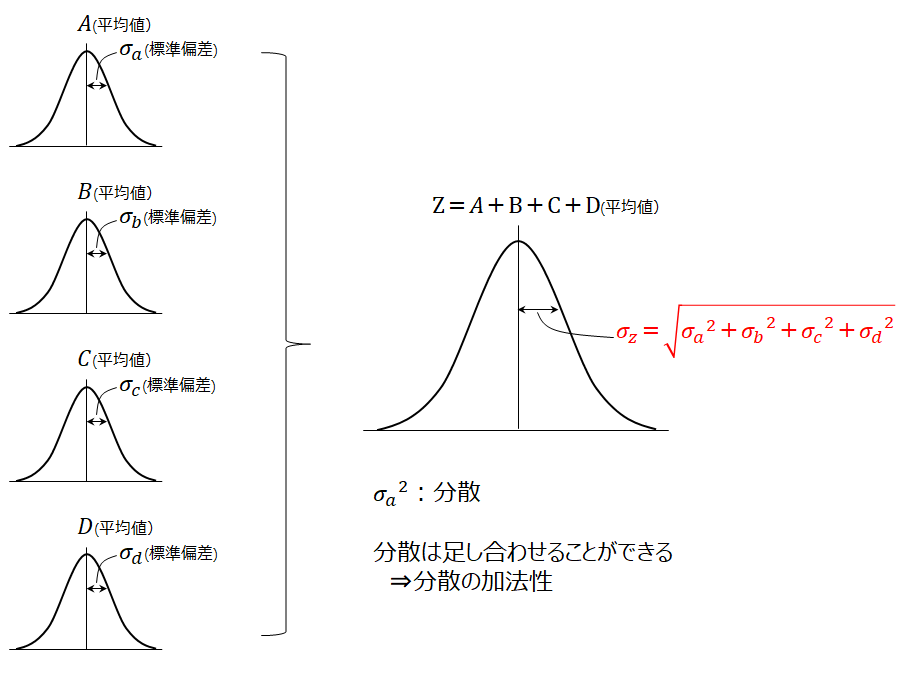
部品A~Dの寸法が正規分布となる場合、それらを組み合わせた時の寸法Zも正規分布となる。分散は足し合わせることができるという性質を持っており(分散の加法性)、寸法Zの標準偏差は以下のように計算することができる。
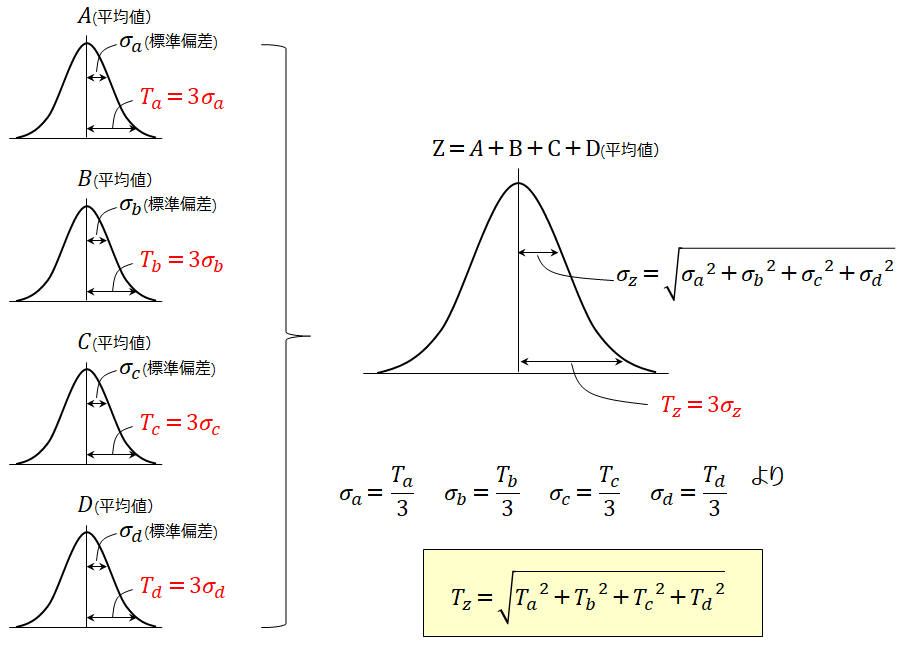
上記の考え方を使うことにより、寸法Zの累積公差を統計的に計算することができる。部品A~Dの寸法公差がそれぞれの標準偏差の3倍だと仮定すると、累積公差Tzも標準偏差の3倍となる。
上記の説明で分かるように、組み合わせる部品が正規分布でない場合、この方法を使うことはできない。NC工作機のような機械で大量に作り、バラツキが十分に把握できているようなケースで採用する方法である。また、Tzも統計上不良率が0.3%発生することを意味するので、不良が発生した時の被害の程度が大きい場合は、よく検討した上で採用すべきである。
スポンサードリンク
【参考文献】
栗山弘 『公差設計入門』 日経BP
※非常に詳しく書かれており分かりやすいです。
最終更新 2018年2月28日