2018年2月にプラスチックス・ジャパン.comに寄稿した記事を掲載します。
1. はじめに
プラスチック製品の強度設計をする上で、ヤング率（縦弾性係数）と材料の強さを確認することは欠かせない作業である。プラスチックの物性表を見てみると、ヤング率と材料の強さを示す項目に、引張試験で測定したものと、曲げ試験で測定したものがあることに気づく。強度設計を行う際に、どちらの値を使えばよいのだろうか。今回は引張特性の規格であるJIS K7161-1、曲げ特性の規格であるJIS K7171に基づき、両特性の概要と強度設計における注意点について解説する。
2. ヤング率
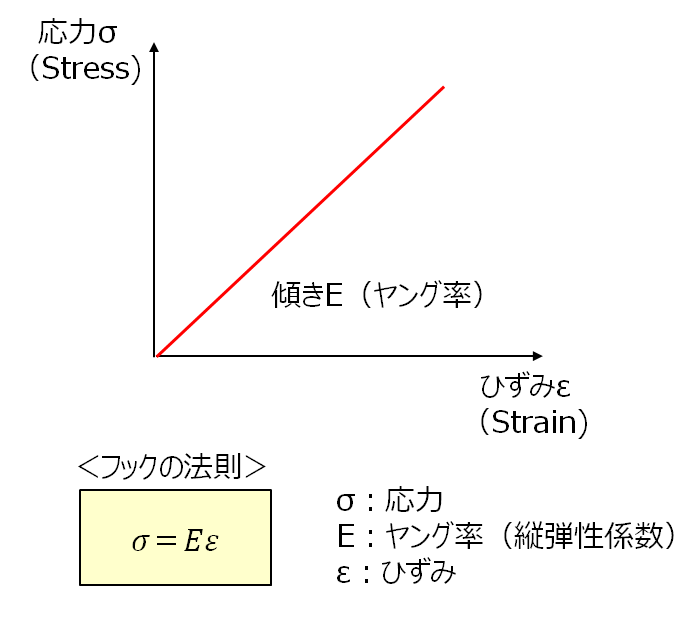
材料の変形のしにくさを示す物性値がヤング率である。材料が弾性変形をする場合、応力とひずみは比例関係となり、ヤング率はその直線の傾きを表す（フックの法則）（図1）。
図1 フックの法則とヤング率
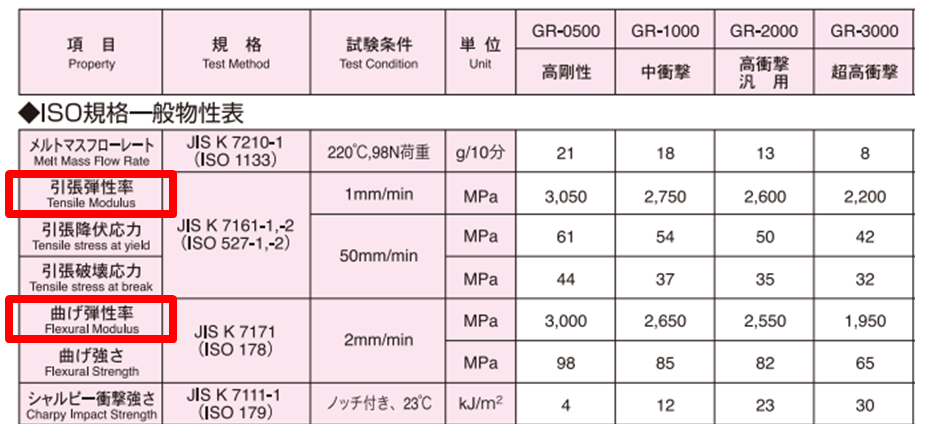
プラスチックの物性表では、ヤング率あるいは縦弾性係数という言葉を見かけることは少ない。代わりに使われるのが引張弾性率または曲げ弾性率である（図2）。
図2 物性表における引張弾性率と曲げ弾性率
（出所：デンカ 「デンカABS 一般物性表」）
引張試験で測定したヤング率が引張弾性率、曲げ試験で測定したヤング率が曲げ弾性率である。両者の違いについては後述する。
スポンサードリンク
3. 材料の強さ
弾性材料の場合、応力とひずみの関係は図1のように直線状になるが、実際には材料の種類や測定条件によって様々な曲線を描く。応力とひずみの関係をグラフ上にプロットしたものを応力－ひずみ曲線（S－S曲線）と呼び、材料の特性を示すために用いられる。材料の強さは応力－ひずみ曲線を使って定義されている。
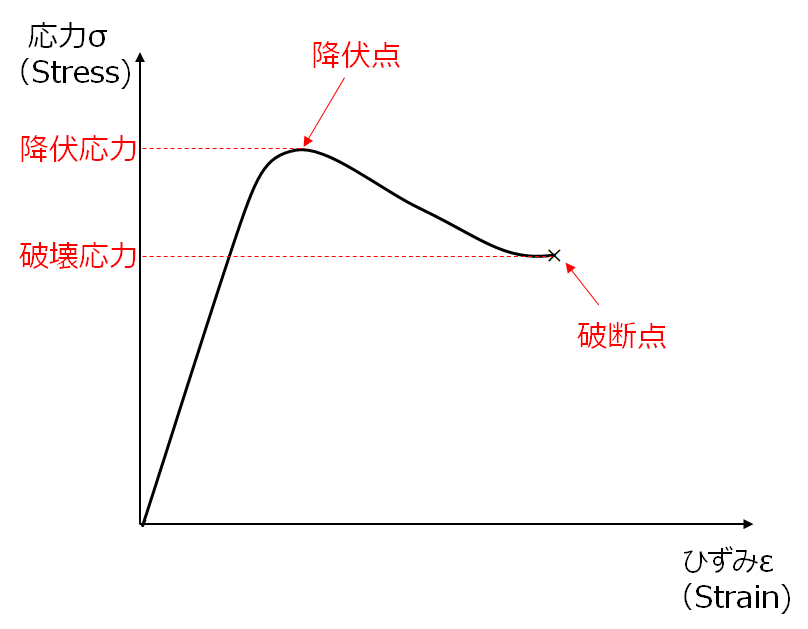
図3 応力－ひずみ曲線と材料の強さ
応力が増えずにひずみが増える最初の部分（曲線の凸部分）を降伏点、その時の応力を降伏応力という。また、材料が破断する時の応力を破壊応力という。材料によって降伏点が現れるものと現れないものがあり、降伏点が現れるものは降伏応力を、降伏点が現れないものは破壊応力を材料の強さとすることが多い。プラスチックの強さを表す用語はJISで表1のように定義されている。
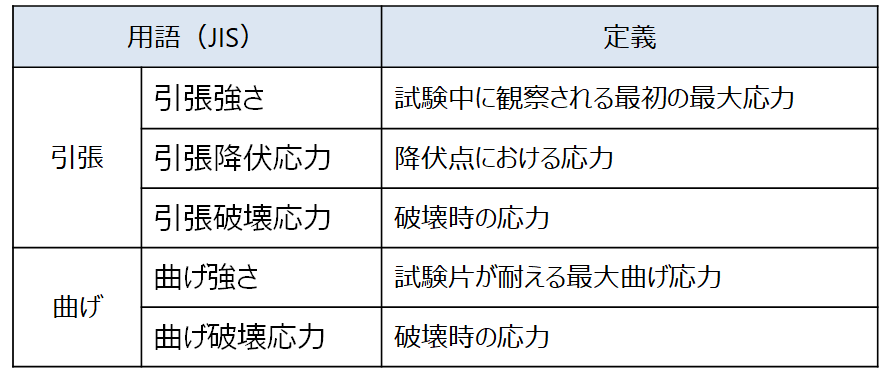
表1 JISにおけるプラスチック材料の強さを示す用語
表1の定義は少し分かりにくいところもあるが、一般に以下のようにいえる。
【引張特性】
降伏点あり → 引張強さ＝引張降伏応力
降伏点なし → 引張強さ＝引張破壊応力
【曲げ特性】
降伏点あり → 曲げ強さ＝降伏応力
（※JIS K7171に「曲げ降伏応力」という用語の定義はない）
降伏点なし → 曲げ強さ＝曲げ破壊応力
プラスチックの物性表では、材料の特性などに合わせて、表1のいずれかの強さが示される。図4では「引張降伏応力」、「引張破壊応力」、「曲げ強さ」が使われている。
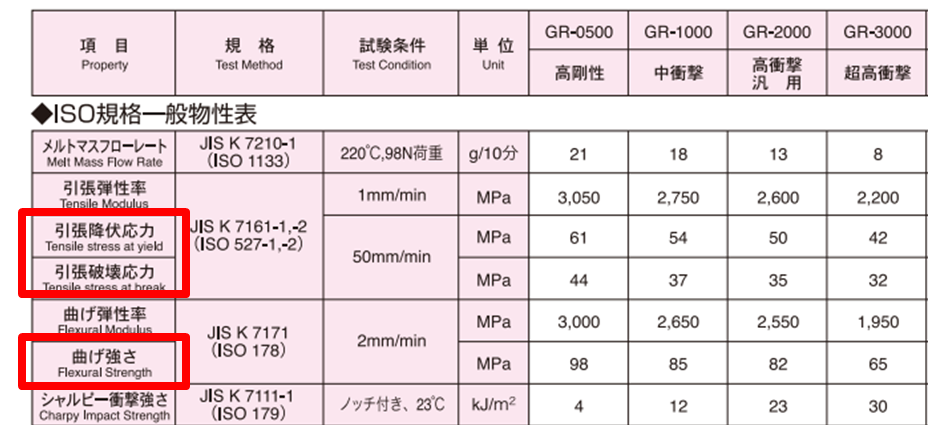
図4 プラスチック材料の強さ
（出所：デンカ 「デンカABS 一般物性表」）
 | 『製品設計知識 e-learning』 ＜設計者のための＞ プラスチック材料特性入門 |
| 期間限定で無料公開中です。ぜひご受講ください。 |
4. 引張特性と曲げ特性の測定方法
＜引張特性＞
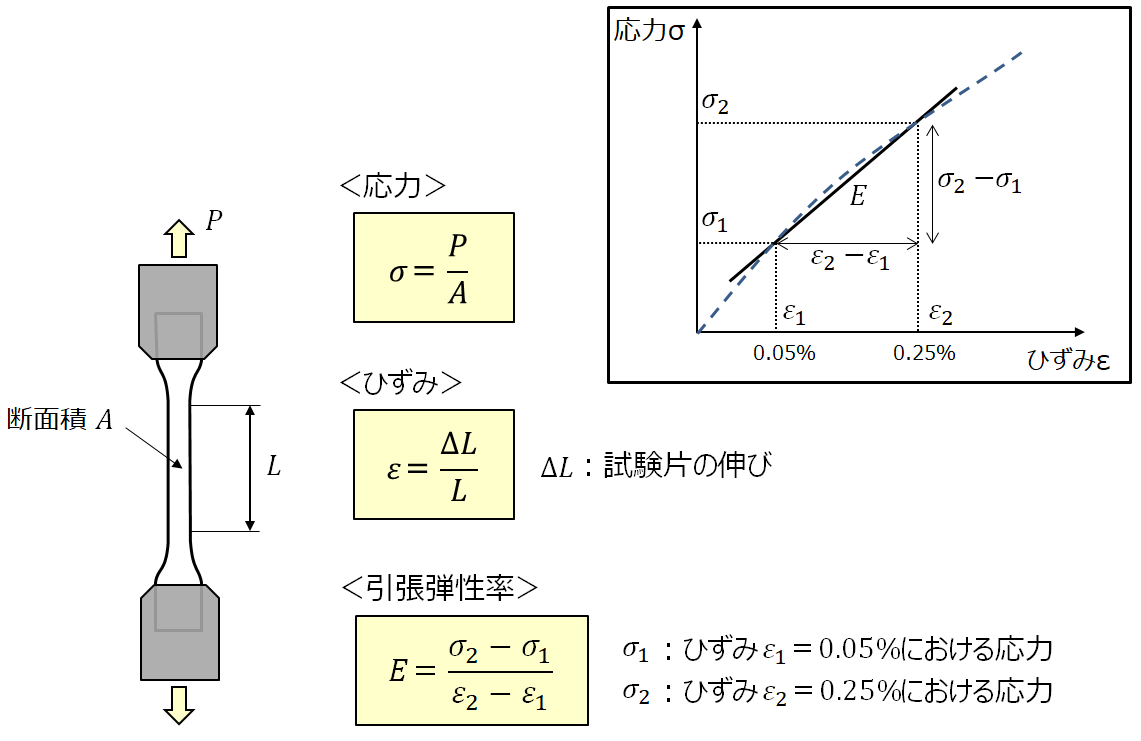
引張特性は図5のような試験で測定し、計算式で算出した応力とひずみを応力－ひずみ曲線にプロットすることによって導く。
図5 引張特性の測定と算出
応力は荷重を試験片の断面積で除したもの、ひずみは試験片の伸びを元の長さで除したものである。引張弾性率は微小な変形時（ひずみが0.05％、0.25％の2点）における、応力－ひずみ曲線の傾きを求めることにより算出する。
＜曲げ特性＞
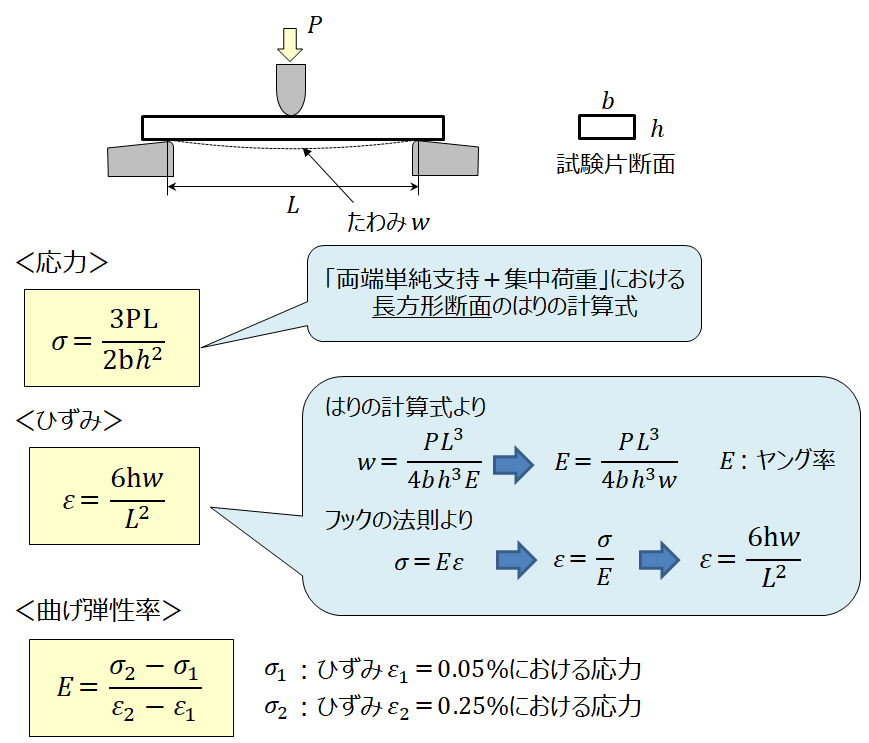
曲げ特性は図6のような3点曲げ試験で測定し、計算式および応力－ひずみ曲線にプロットすることによって導く。
図6 曲げ特性の測定と算出
曲げ特性における応力とひずみは、前回解説したはりの強度計算における「両端単純支持＋集中荷重」における長方形断面の計算式を適用することによって求められる。曲げ弾性率は引張弾性率と同様に、微小な変形時（ひずみが0.05％、0.25％の2点）における、応力－ひずみ曲線の傾きを求めることにより算出する。
＜前回解説記事＞
製品設計の「キモ」(17)～ プラスチック製品設計における「はりの強度計算」の活用
https://plastics-japan.com/archives/3302
＜参考記事＞
はりの強度計算ツール（応力・ひずみ・たわみの計算）
スポンサードリンク
5. 強度設計における注意点
プラスチックの物性表には引張特性、曲げ特性の両者が掲載されていることは既に述べた。引張特性と曲げ特性では試験方法や算出方法が異なるものの、求めているヤング率や材料の強さは同じもののようにも思える。それでは、強度設計を行う場合、どちらを使えばよいのだろうか。
曲げ特性の規格JIS K7171では以下のように述べられている。
＜JIS K7171＞
『この試験方法は、プラスチックの設計パラメータの決定には適切ではないが、材料比較試験及び品質管理のための試験として使用できる。』
つまり曲げ特性を使って強度設計を行うことは好ましくないということである。その理由について考えてみよう。
曲げ試験において試験片には図7のような応力が生じている。
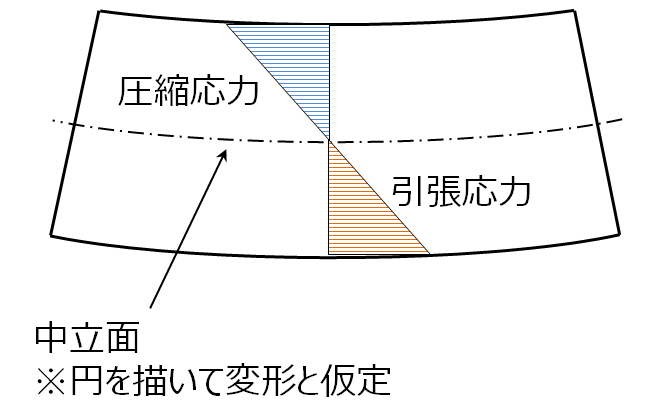
図7 曲げ試験において試験片に生じる応力
中立面より上側には圧縮応力、下側には引張応力が生じている。上下ともに応力は一番外側で最も大きい。曲げ試験における物性値は、試験片の一番外側の物性値に大きな影響を受けることになる。プラスチックは材料の種類、成形条件、試験片の厚みなどによって、厚み方向で物性値に違いが生じるため、曲げ試験で得られる物性値の精度は低くなることが分かるだろう。
また、はりの計算式は材料が弾性体かつ均質であり、円を描くように変形するという前提で導かれている。プラスチックは圧縮と引張のヤング率に違いがあることや、試験片が完全な円を描いて変形しないことなどが原因で、はりの計算式で算出した物性値の精度は高くない。さらに、ひずみが大きくなるほど計算式の前提は崩れていくため、精度はより低くなっていく。
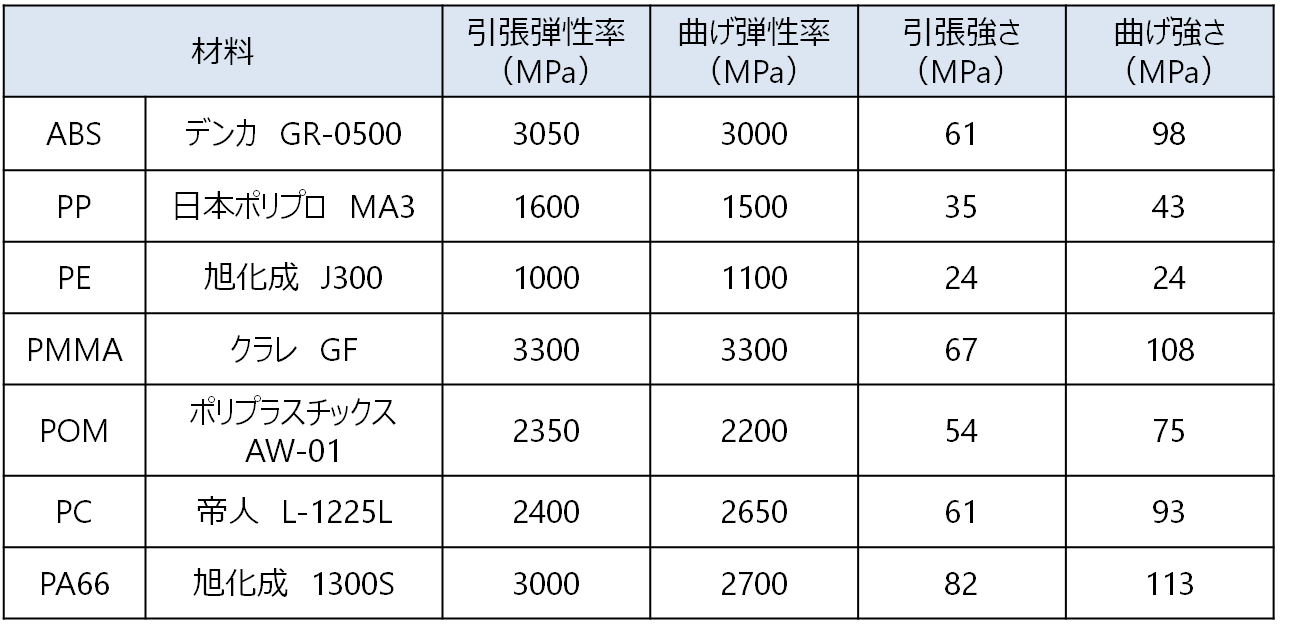
表2は実際の材料における引張特性と曲げ特性の比較である。同じ材料でも引張と曲げで異なった値を示すことが分かる。
表2 引張特性と曲げ特性の比較
（出所：各材料メーカー物性表）
ヤング率は微小な変形時における値であるため、両者に差はあるものの、引張弾性率と曲げ弾性率の差は比較的小さい。しかし、材料の強さについては、変形量が大きい時の値であるため、引張強さと曲げ強さに大きな差を生じてしまう。しかも、曲げ強さは引張強さよりかなり高めに出ることが多いため、強度設計で曲げ強さを使用することは避けなければならない。
これらの理由により、強度設計においては曲げ特性ではなく、引張特性を用いるというのが原則であるといえる。
6. おわりに
プラスチック材料における引張特性と曲げ特性についての概要を解説した。両者の違いを理解した上で強度設計を行うことが重要である。
【参考文献】
JIS K7161-1:2014 「プラスチック−引張特性の求め方－第 1 部：通則」
JIS K7171:2016 「プラスチック−曲げ特性の求め方」
本間精一 『プラスチック材料大全』 日刊工業新聞社
有方広洋 『プラスチック成形加工基礎と実務』 日刊工業新聞社